L1, L2 regularization demystified.

I decided to write about L1, L2 regularization out of frustration in finding intuitive explanation online. It’s probably buried deep inside some statistics or machine learning courses, but if you only have 5 minutes, and about to have your next nerve wrecking data science job interview, then you are doomed.

Let me head straight to the conclusion now. You will get sparsity in your parameters with L1, but the exact opposite with L2, period. Everyone who has been through enough interview can give you the answer. But why is that the case? It is not obvious just by looking at the formula.

Let’s say you want to find the optimal solution to a regression problem to a general, nonlinear function $f$ by minimizing the following formulae. In the case of L1,

$\text{Loss}_{\text(L1)} = \text{MSE}(D, \mathbf{w}) + \text{L1}(\mathbf{w}) = \sum_{i=1}^{n} (f(x_i;\mathbf{w}) - y_i)^2 + \lambda \sum_{j=1}^k |w_j|.$

And in the case of L2,

$\text{Loss}_{\text(L2)} = \text{MSE}(D, \mathbf{w}) + \text{L1}(\mathbf{w}) = \sum_{i=1}^{n} (f(x_i;\mathbf{w}) - y_i)^2 + \lambda \sum_{j=1}^k w_j^2.$

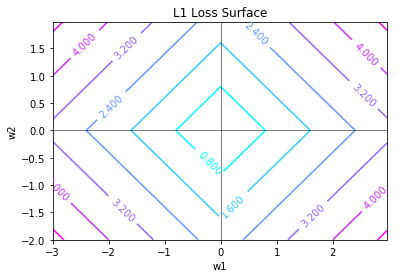
It is not immediately obvious why L1 gives you sparsity of $\mathbf{w}$. The answer will become clear once we consider the error surfaces of the two terms in the loss formula seperately in the parameter space. First, let’s consider the contour of the L1 error surface; this is where only the $|\mathbf{w}|$ term is presented.

$g(w) = \sum_{j=1}^k |w_j|.$

The contour shows up diamond-shaped, and the diamond grows larger as the error increases. Each line is called the L1 circle. Why is it called “circle”? Imagine you are an alien who can only measure distance of a point to the origin by using a tool perpendicular to the axes and summing the measurements, then every point in the line will have equal distance to the center. The L1 function, $g$ defines exactly the distance to center.

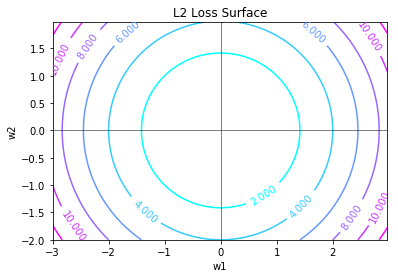
Similarly, the L2 equation will give us our regular “circle”, as the formula defines exactly the euclidean distance.

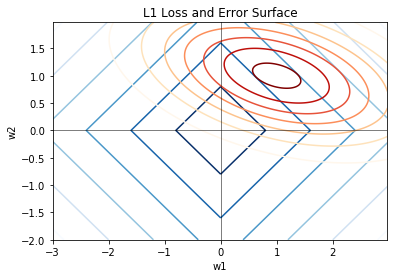
Now, what happens when you have another competing error term? We can check in the following figure; the error surface (for instance, MSE) is colored in orange red. The regularization term and the error term are competing because when you optimize the loss you are finding a point in the parameter space where the sum of the two terms are the minimum. When one losses, the other grows, so the terms are basically “competing” for a position during optimization. If you change the regularization “strength”, $\lambda$, the cometition changes, and the global optimum settle to a different point.

The sparsity of the L1 term comes from the fact that the diamond shape has a higher chance of settling to any of the corners during optimization. In the 2d case, finding optimum in the corner means that one of the parameter is zero. Imaging in multidimensional case, the corners will be hyper corners, where only some of the parameters are zero. These corners are the cause of the sparsity during optimization.

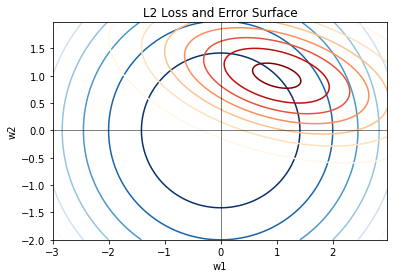
If you look at the L2 surface, the cometition changes. The L2 surface does not favor the corner; L2 can settle at any angle of the circle, making all of the weight terms non-zero.

So, if you want to do feature selection, go with L1 regularization. The exact opposite applies to L2; that is, L2 will tend to preserve all the terms in your parameters. As some say they tend to see performance boost using L2; they are most likely overfitting by memorizing their data in the parameter space.

Some useful links.